Referensi dari buku: Introduction to fuzzy sets, fuzzy logic, and fuzzy control systems / Guanrong Chen, Trung Tat Pham
pengontrol
PID konvensional: konfigurasinya, metode desain, dan analisis stabilitas, yang
akan dibutuhkan dalam memperkenalkan PID fuzzy pengontrol nanti, di mana
pengontrol PID fuzzy adalah ekstensi alami dari yang konvensional: mereka
memiliki struktur yang sama tetapi didefinisikan berdasarkan matematika fuzzy
dan strategi kontrol fuzzy. Secara individual, proporsional konvensional (P), integral
(I), dan turunan (D) pengontrol untuk mengendalikan sistem tertentu (pabrik,
proses) memiliki:
di mana r = r(t) adalah input referensi (set-point), y =
y(t) adalah output sistem yang dikendalikan, e = e(t) := r(t) – y(t) adalah
kesalahan pelacakan set-point, dan u = u(t) adalah kontrol action (output dari
controller) yang digunakan sebagai input ke sistem.
Dimana :
2. Fuzzy PID Controllers Design [Kembali]
Kontroler fuzzy PD, PI, dan PI+D yang akan diperkenalkan di bawah ini adalah perpanjangan alami dari versi konvensionalnya.
A. Fuzzy PD Controller
Keseluruhan sistem kontrol pelacakan titik setel fuzzy PD ditunjukkan pada Gambar di bawah, di mana proses yang dikendalikan adalah sistem waktu-diskrit (atau sistem waktu-kontinu terdiskritisasi), dan r(nT) adalah sinyal referensi yang dapat menjadi konstan (set point). Kontroler PD fuzzy di dalam kotak putus-putus berbeda dari kontroler PD digital konvensional (ditunjukkan pada Gambar 5.7) dalam hal ada "kontroler fuzzy" tambahan di jalur sinyal kontrol inkremental u(nT). Selain itu, blok perkalian konstan telah diubah dari
periode sampling T ke gain kontrol konstan yang dapat disesuaikan Ku untuk memungkinkan pengontrol baru satu derajat kebebasan lagi dalam proses kontrol
Untuk mengilustrasikan bagaimana blok “pengontrol fuzzy” bekerja, pertama-tama kita memperkenalkan parameter konstan (skalar yang dapat disesuaikan) L > 0, dan menguraikan bidang dengan L sebagai dua puluh wilayah kombinasi input (IC1-IC20) seperti yang ditunjukkan pada Gambar 5.9, di mana sumbu horizontal adalah sinyal input Kpd(nT), dan sumbu vertikal adalah sinyal input Kdv(nT), ke "pengendali fuzzy." Kemudian, menurut wilayah mana sinyal input (Kpd(nT), Kdv(nT)) termasuk, blok "pengendali fuzzy" menghasilkan output tambahan berikut:
Pada langkah fuzzifikasi, kami menggunakan dua input: sinyal kesalahan e(nT) dan laju perubahan sinyal kesalahan v(nT), dengan hanya satu keluaran kontrol u(nT) (untuk diumpankan ke sistem yang dikendalikan) . Input ke kontroler PD fuzzy, yaitu sinyal “error” dan “rate”, harus difuzzifikasi sebelum diumpankan ke kontroler. Fungsi keanggotaan untuk dua input (error dan rate) dan output dari pengontrol yang digunakan dalam desain kami ditunjukkan pada Gambar di bawah, yang kemungkinan merupakan fungsi paling sederhana yang mungkin digunakan untuk tujuan ini. Baik error maupun rate memiliki dua nilai keanggotaan: positif dan negatif,
sedangkan outputnya memiliki tiga (fungsi tunggal): positif, negatif, dan nol. Konstanta L > 0 yang digunakan dalam definisi keanggotaanfungsi dipilih oleh perancang sesuai dengan rentang nilai kesalahan, laju, dan keluaran, yang digunakan sebagai parameter yang dapat disetel tetapi juga dapat diperbaiki setelah ditentukan. Perhatikan bahwa konstanta L yang digunakan dalam ketiga fungsi keanggotaan ini dapat berbeda secara umum (menurut arti fisik dari sinyal dalam aplikasi), tetapi kami membiarkannya sama di sini untuk menyederhanakan desain.
Desain kontroler fuzzy PI mirip dengan desain fuzzy PDcontroller, dan akan diperkenalkan secara singkat di subbagian ini.Sistem pengontrol PI secara keseluruhan ditunjukkan pada di bawah. Pada Gambar ini, kita membiarkan Kp = KP dan Ki = KI , seperti yang disebutkan sebelumnya. Kontroler fuzzy bekerja dengan cara yang mirip dengan kontroler PD fuzzy. Pertama kita dekomposisi bidang dengan skalar L > 0 menjadi dua puluh daerah kombinasi input (IC) untuk input Kie(nT) dan Kpv(nT), di mana v(nT) = T1 [e(nT)–e(nT– T)],di sini, Kie(nT) dan Kpv(nT) masing-masing disebut sinyal kesalahan dan laju perubahan sinyal kesalahan, untuk kemudahan. Kemudian, menurut lokasi input (Kie(nT), Kpv(nT)) ke blok “fuzzy controller”, output kontrol inkremental yang sesuai dihitung dengan rumus berikut:
Fuzzy PI Controller
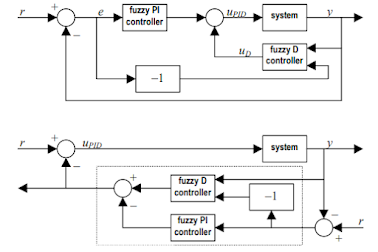
C. Fuzzy PI+D ControllerKontroler PI+D analog konvensional, Serupa dengan desain kontroler fuzzy PD yang dibahas pada Bagian II.A, pertama-tama kita akan melakukan diskritisasi dengan menerapkan transformasi bilinear, kemudian mendesain kontroler fuzzy PI dan fuzzy D secara terpisah, dan akhirnya menggabungkannya secara keseluruhan dalam loop tertutup.Dengan demikian, desain pengontrol fuzzy PI sama dengan itudisebutkan secara singkat di atas, tetapi desain kontroler fuzzy D agak berbeda. Dimulai dengan sistem kontrol PI+D analog konvensional yang ditunjukkan pada Gambar di bawah, output dari kontroler PI analog konvensional dalam domain frekuensi s,
3. Fuzzy PID Controllers: Stability Analysis [Kembali]
Pada bagian ini, kami menganalisis stabilitas fuzzy PI, PD, dan PI+D sistem kontrol yang dirancang dan dipelajari di bagian terakhir. Ingat stabilitas asimtotik Lyapunov untuk pemodelan fuzzy yang dibahas dalam Bab 3, baik untuk sistem dinamis fuzzy waktu-diskrit dan waktu-kontinu. Untuk menunjukkan jenis stabilitas penting lainnya, yaitu stabilitas input terbatas-output terbatas (BIBO) dari sistem kontrol, kami memperkenalkan Teorema Penguatan Kecil di bagian ini dan membahas stabilitas BIBO dari fuzzy PI, PD, dan Sistem kontrol PI+D. Kami pertama mencatat bahwa berbeda dari stabilitas asimtotik Lyapunov, yang biasanya lokal (di lingkungan titik ekuilibrium), stabilitas BIBO bersifat global dan sangat cocok untuk sistem nonlinier yang dijelaskan oleh peta input-output. Kami juga harus mencatat bahwa baik stabilitas asimtotik Lyapunov dan analisis stabilitas BIBO memberikan kondisi yang cukup konservatif, terutama untuk sistem nonlinier. Dari sudut pandang teoritis, semakin besar daerah stabilitas dapat ditemukan, semakin baik hasilnya. Namun, dari sudut pandang desain, wilayah stabilitas yang relatif konservatif sebenarnya lebih aman dan lebih andal dalam aplikasi. Teori stabilitas BIBO ternyata tepat untuk tujuan ini.
A. BIBO Stability and the Small Gain TheoremSuatu sistem kontrol (linier atau nonlinier) dikatakan stabil dengan input terbatas-output (BIBO) jika input kontrol yang dibatasi ke sistem selalu menghasilkan output terbatas melalui sistem.batasnya didefinisikan dalam norma (l2, l∞, dll.) dari fungsi ruang yang kami pertimbangkan dalam desain.Misalkan S menyatakan sistem (linier atau nonlinier). S dapat dianggap sebagaipemetaan yang memetakan input kontrol, u(t), ke output sistem yang sesuai y(t), di mana
di mana "ess" berarti "essential", yaitu, supirum memegang kecuali lebih dari satu set ukuran nol. Untuk sinyal terus menerus sepenggal, supirum esensial dan supirum sama, jadi "ess" bisa diturunkan dari atas.
B. BIBO Stability of Fuzzy PD Control Systems
3. Fuzzy PID Controllers: Stability Analysis [Kembali]
di mana "ess" berarti "essential", yaitu, supirum memegang kecuali lebih dari satu set ukuran nol. Untuk sinyal terus menerus sepenggal, supirum esensial dan supirum sama, jadi "ess" bisa diturunkan dari atas.














No comments:
Post a Comment